Corban Harwood, PhD
Chair, Department of Mathematics
Professor of Mathematics

As a mathematician and scientist, I stand in awe of God’s handiwork. Mathematics is a gift from God and a language of creation. Since I was young, I have always been intrigued by how mathematics can be used to translate things we experience like movement, sound, and patterns into a coherent form based on reason and logic. What are the mathematics that our brain "does" when we listen to music? Why does nature mimic mathematical patterns?
These are the kinds of questions which drew me into mathematics, but it was the dichotomy of logical simplicity and infinite complexity which has kept my attention. As a professor, I love sharing this passion with my students and helping them see the beauty and utility of mathematics. I began teaching at George Fox University in 2011 and feel blessed to "Be Known" by the students as well as the faculty and staff. I enjoy being a part of this community which nurtures students' hearts and minds, and allows me to integrate my faith.
Academic Background
- BS, Mathematics, Whitworth University (2006)
- MS, Mathematics, Washington State University (2008)
- PhD, Mathematics, Washington State University (2011)
Research Interests
My research focus is in the area of Numerical Partial Differential Equations. I develop and analyze algorithms which can be used to approximate solutions to multivariable differential equations which are numerically stable and free of unwanted oscillations. Such equations can model various phenomena from the reaction and diffusion of chemicals to the propagation of waves. In short, I analyze the underlying components of an algorithm to predict its long term behavior. I seek the optimal conditions which produce solutions that are trustworthy and feasible, while simultaneously minimizing error and computational time.
Along with my doctoral research at Washington State University, I worked for a battery design center at the University of Idaho, developing models and simulations to predict optimal design specifications. Currently at George Fox University, I help students seek out research and internship experience and enjoy working with several students on my own research projects. Such experience is critical in developing professional skills for young mathematicians.
In analyzing algorithms, I sometimes stumble upon dazzling artwork. Often when solutions are not dependable to solve a given problem, their behavior can be quite beautiful. Below are a fractal displaying the chaotic sensitivity of Newton's method to starting values and a graph showing how eigenvalues spread within a contained region as the step sizes of an algorithm are varied.
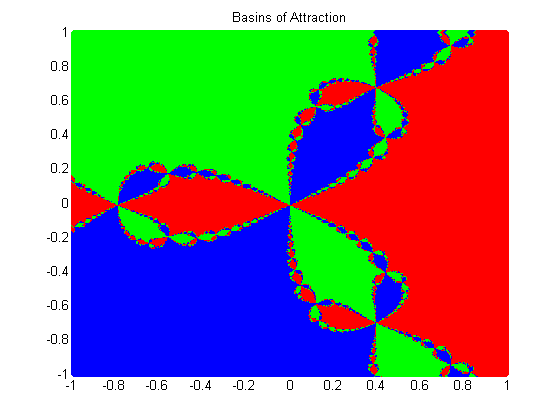
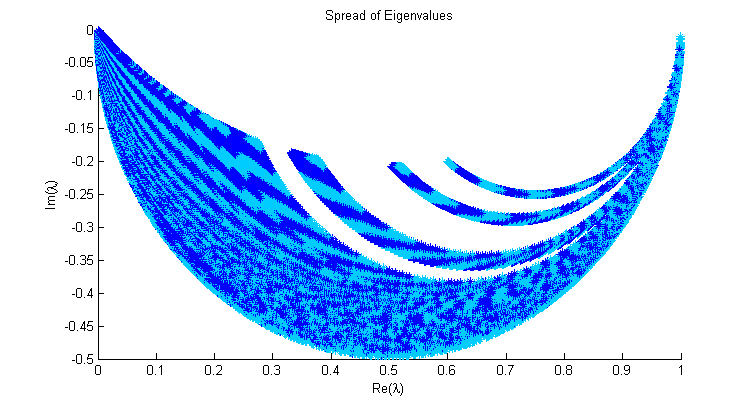
Select Research Bibliography
Published Scholarship on George Fox University's Digital Commons
Primary Teaching Responsibilities
- MATH 201/202/301 - Calculus
- MATH 311 - Differential Equations with Linear Algebra
- MATH 312 - Numerical Methods
- MATH 411 - Advanced Linear Algebra
Outside the Classroom
In front of all the mathematical research that I am passionate about, my wife, Mary, and my children, Elizabeth and Christopher, take center stage. Mary and I grew up in Washington (Mary) and Montana (me) and have now lived in Newberg since 2012. We all share a love for the outdoors, music, and the culinary arts. You may catch us on a family hike at Champoeg park or walking downtown for the Art Walk every first Friday. We enjoy exploring the natural beauty of God's creation, especially the Willamette Valley, Oregon Coast, and Cascade range nearby. In addition to hiking and camping, I love the challenging hill climbs and gorgeous views while riding my bike around Newberg. At home, I also enjoy playing and analyzing games, and reading science fiction and fantasy novels.